Понятия фрактал и фрактальная геометрия, появившиеся в конце 70-х, с середины 80-х прочно вошли в обиход математиков и программистов. Понятие фрактала, введенное в научный обиход Бенуа Мандельбротом, не имеет строгого определения. Согласно Мандельброту, слово фрактал происходит от латинских слов fractus - дробный и frangere - ломать, что отражает суть фрактала, как "изломанного", нерегулярного множества. Определение фрактала, данное Мандельбротом, звучит так: «Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому». Любая попытка дать более строгое определение отсекает какой-то достаточно емкий класс объектов, непозволительно сужая мир фракталов.

Простейшие фракталы, такие, как снежинки фон Коха, губка и треугольник Серпинского, кривые дракона, кривые Пеано и многие другие, обладают регулярной геометрически правильной структурой. Каждый фрагмент такого геометрически правильного фрактала в точности повторяет всю конструкцию в целом. Часть фрактала имеет туже структуру или форму, как и целое, за исключением того, что они при различном масштабе могут немного искажаться. Форма сильно неправильна и фрагментирована, и остается такой независимо от масштаба.

При менее точном следовании самоподобию возникают другие, например, случайные фракталы, в которых подобность заключается в сохранении нормальности случайного распределения на разных масштабах. Примерами случайных фракталов могут служить пограничные и береговые линии, поры в хлебе, дырки в некоторых сортах сыра, частицы в порошках и т.д.

Итак, что же такое фрактал?

Как уже говорилось, этот термин принадлежит Бенуа Мандельброту. В трех своих книгах Бенуа Мандельброт предложил изумленному миру по существу новую неевклидову геометрию. Он создал неевклидову геометрию негладких, шероховатых, зазубренных, изъеденных ходами и отверстиями, шершавых и т.п. объектов, своего рода математических парий, который почему-то изгонялись из рассмотрения в пользу более благообразных усредненных, сглаженных, отполированных, спрямленных объектов. Между тем именно «неправильные» объекты составляют подавляющее большинство объектов в природе.

«Фрактальная геометрия природы» Б.Мандельброта

открывается следующими словами: «Почему геометрию часто называют "холодной" и "сухой"? Одна из причин заключается в ее неспособности описать форму облака, горы, береговой линии или дерева. Облака - не сферы, горы - не конусы, береговые линии - не окружности, древесная кора не гладкая, молния распространяется не по прямой».

Красота фракталов двояка:

--она услаждает глаз (и слух), о чем свидетельствует хотя бы обошедшая весь мир выставка фрактальных изображений, организованная группой математиков под руководством Пайтгена и Рихтера. Позднее экспонаты этой грандиозной выставки были запечатлены в иллюстрациях к книге тех же авторов «Красота фракталов».

-- но существует и другой, более абстрактный или возвышенный, аспект красоты фракталов, открытый, по словам Р.Фейнмана, только умственному взору теоретика, в этом смысле фракталы прекрасны красотой трудной математической задачи.

Красота фракталов сочетает в себе красоту симметричных объектов типа кристаллов с красотой "живых" природных объектов, привлекательных именно своей неправильностью. Фракталы с большой точностью описывают многие физические явления и образования реального мира: облака, горы, кровеносные сосуды, турбулентные течения, береговые линии, корни, ветки деревьев, легкие животных, что далеко не соответствует простым геометрическим фигурам, при фрактальном подходе хаос перестает быть синонимом беспорядка и обретает тонкую структуру. И поэтому мы можем вслед за Б.Мандельбротом с полным правом говорить о фрактальной геометрии природы.

Свойства фракталов

Фрактальные объекты обладают необычными свойствами. Длины, площади и объемы одних фракталов равны нулю, других - обращаются в бесконечность. Одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала содержит информацию о всем фрактале. Структура фракталов настолько сложна, что оставляет заметный отпечаток на физических процессах, протекающих на фракталах как на носителях. Фракталы иначе рассеивают электромагнитное излучение, по-другому колеблются и звучат, иначе проводят электричество, по фракталам иначе происходит диффузия вещества. Возникает новая область естествознания - физика фракталов. Фракталы становятся удобными моделями для описания процессов в средах, ранее считавшихся неупорядоченными.

Классификация фракталов

Для чтобы представить все многообразие фракталов удобно прибегнуть к их общепринятой классификации.

Геометрические фракталы

Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.

Рассмотрим один из таких фрактальных объектов - триадную кривую Кох. Построение кривой начинается с отрезка единичной длины - это 0-е поколение кривой Коха.

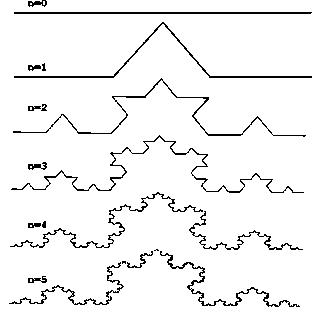
Далее каждое звено (в нулевом поколении один отрезок) заменяется на образующий элемент, обозначенный на рис.2 через n=1. В результате такой замены получается следующее поколение кривой Коха. В 1-ом поколении - это кривая из четырех прямолинейных звеньев, каждое длиной по 1/3. Итак, для получения каждого последующего поколения, все звенья предыдущего поколения необходимо заменить уменьшенным образующим элементом. Кривая n-го поколения при любом конечном n называется предфракталом. На рисунке представлены пять поколений кривой. При n стремящемся к бесконечности кривая Коха становится фрактальным объектом. Если взять за основу не прямую, а треугольник и применить тот же алгоритм для каждой из сторон, то мы получим снежинку Коха.

 Если самое первое слева звено заменяется на образующий элемент так, чтобы середина звена смещалась влево от направления движения, а при замене следующих звеньев, направления смещения середин отрезков должны чередоваться, то мы полуим Предельную фрактальную кривую (при n стремящемся к бесконечности), называющуюся «драконом» Хартера-Хейтуэя. На рисунке представлены несколько первых поколений и 11-е поколение кривой, построенной по вышеописанному принципу.

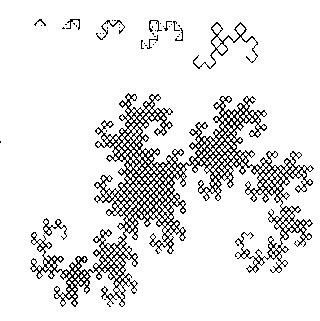
     Алгебраические фракталы

Это самая крупная группа фракталов. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные небанальные структуры.

Примером таких фракталов может служить:

Множество Мандельброта

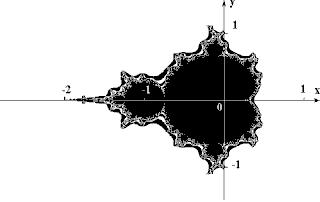
  Участок границы множества Мандельброта, увеличенный в 200 pаз.

Кривая Пеано

Треугольник Серпинского

Лоренцевы аттракторы